企業博客
更多>>有源晶振啟動時間
來源:http://m.bsgccc.com 作者:康比電子 2019年04月27
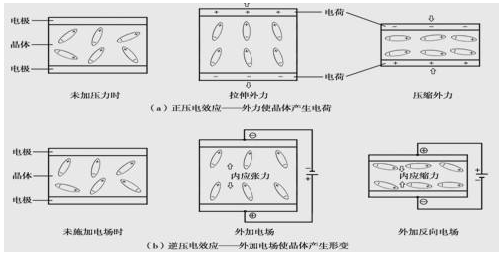
壓電石英晶體是電子產品不能缺少的"心臟",更無法想象沒有石英晶振的世界會是怎樣的.其實有很多方法可以用一塊石英切割晶體諧振器.AT切割晶體因其良好的溫度系數特性和從一個樣品到另一個樣品的一致性而廣受歡迎.晶體因其高品質因數(QF)而廣泛用于振蕩器,時基和頻率合成器;出色的頻率穩定性,嚴格的生產公差;而且成本相對較低.下面康比電子介紹關于有源晶振啟動時間及頻率穩定性與溫度技術資料.
啟動時間
有源晶振的啟動時間的定義可以根據系統的類型而變化.對于微處理器系統,啟動時間通常是從初始功率應用到穩定時鐘信號可用的時間.鎖相環(PLL)的啟動時間通常是從初始功率施加到穩定參考信號可用時的時間,通常穩定在距最終穩態振蕩頻率的可接受頻率偏移內.晶體振蕩器的啟動時間取決于開啟時的噪聲或瞬態條件;由于負電阻導致的小信號包絡擴展;和大信號限幅.
包絡擴展僅是總負阻和晶體的運動電感的函數.簡化的等效串聯LCR電路包含運動電感,三點振蕩器的施加負電阻和晶體的運動電阻之和,以及整個網絡的有效串聯電容(由運動電容支配).未驅動的網絡可以使用以下方式建模:
s*L+R+1/(s*C)=0
將兩邊乘以s/L給出:
s2+s*(R/L)+1/(L*C)=0
根位于:
½*{-R/L±√[(R/L)2-4/(L*C)]}
因為平方根內的R/L項被1/(L*C)項淹沒,所以方程可以簡化為
-R/(2*L)±-j*√[1/(L*C)]
因為凈電阻R是負的,所以極點在右半平面中.由此產生的微分方程的時域解是:
V(t)=K*[e|(R/2*L)|*t]*sin{2Πt√[1/(L*C)]+Θ} 其中K是常數,Θ是任意相,兩者都與初始啟動條件有關.指數擴展僅對小信號條件有效,因為電路可用的功率有限.
包絡擴展的時間常數是正的.它與三點石英晶體振蕩器的凈負電阻和動態電阻成正比,與運動電感成反比.由于晶體的大運動電感和有限的凈負電阻,晶體振蕩器具有較長的啟動時間.
作為包絡擴展時間常數的一個例子,假設一個具有5-fF運動電容的晶體和一個具有1500-Ω負電阻的振蕩器,工作頻率為10MHz.從動態電容和工作頻率,50.7毫亨的動態電感可以用L=1/(C*ω來計算2).該運動電感產生包絡擴展時間常數t=2*L/|R|=67.55μs.
在降低頻率牽引(由于低運動電容)和較長啟動時間(由于高運動電感)之間存在折衷,因為高運動電感是低運動電容的結果.(兩者的乘積或多或少是固定的.)這種相互依賴性部分地通過較小的運動電容與較小的并聯電容相關聯來減輕,這產生較大的負電阻并由此改善啟動時間.
啟動時間是電池供電應用中的一個重要考慮因素,其中設備經常打開和關閉.較短的振蕩器啟動時間可減少低功率無線電系統(例如使用MAX7032收發器和MAX1472或MAX7058發射器的系統)的能源浪費.
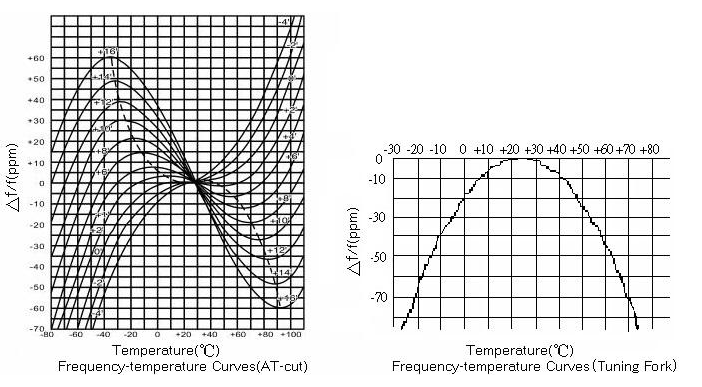
頻率穩定性與溫度 隨著溫度的變化,所有晶振的共振頻率都不同.頻率變化的方式取決于切割晶體的角度.AT切割石英晶振的相對頻移與溫度的關系可以表示為三次多項式.
Δf/f0=A0+A1(T-T0)+A2(T-T0)2+A3(T-T0)3
其中系數A0至A3是切割角度的函數.
頻率穩定性在使用晶體作為頻率參考的系統中很重要.對于高頻窄帶應用尤其如此.考慮863至870MHz歐洲ISM頻段中的25kHz信道.頻率漂移僅為5kHz(小于6ppm)可能導致通信故障或法規不合規.
即使在零容差晶體完全切割且不老化的情況下,在-40°C至85°C的耐高溫晶振中的"工業規格"溫度范圍內保持漂移遠低于6ppm也是不可能的.在這種情況下,帶有內部溫度傳感器和窄頻步分數N合成器的無線電系統,如MAX7049發射器,可用于補償已知的溫度變化.
啟動時間
有源晶振的啟動時間的定義可以根據系統的類型而變化.對于微處理器系統,啟動時間通常是從初始功率應用到穩定時鐘信號可用的時間.鎖相環(PLL)的啟動時間通常是從初始功率施加到穩定參考信號可用時的時間,通常穩定在距最終穩態振蕩頻率的可接受頻率偏移內.晶體振蕩器的啟動時間取決于開啟時的噪聲或瞬態條件;由于負電阻導致的小信號包絡擴展;和大信號限幅.
包絡擴展僅是總負阻和晶體的運動電感的函數.簡化的等效串聯LCR電路包含運動電感,三點振蕩器的施加負電阻和晶體的運動電阻之和,以及整個網絡的有效串聯電容(由運動電容支配).未驅動的網絡可以使用以下方式建模:
s*L+R+1/(s*C)=0
將兩邊乘以s/L給出:
s2+s*(R/L)+1/(L*C)=0
根位于:
½*{-R/L±√[(R/L)2-4/(L*C)]}
因為平方根內的R/L項被1/(L*C)項淹沒,所以方程可以簡化為
-R/(2*L)±-j*√[1/(L*C)]
因為凈電阻R是負的,所以極點在右半平面中.由此產生的微分方程的時域解是:
V(t)=K*[e|(R/2*L)|*t]*sin{2Πt√[1/(L*C)]+Θ} 其中K是常數,Θ是任意相,兩者都與初始啟動條件有關.指數擴展僅對小信號條件有效,因為電路可用的功率有限.
包絡擴展的時間常數是正的.它與三點石英晶體振蕩器的凈負電阻和動態電阻成正比,與運動電感成反比.由于晶體的大運動電感和有限的凈負電阻,晶體振蕩器具有較長的啟動時間.
作為包絡擴展時間常數的一個例子,假設一個具有5-fF運動電容的晶體和一個具有1500-Ω負電阻的振蕩器,工作頻率為10MHz.從動態電容和工作頻率,50.7毫亨的動態電感可以用L=1/(C*ω來計算2).該運動電感產生包絡擴展時間常數t=2*L/|R|=67.55μs.
在降低頻率牽引(由于低運動電容)和較長啟動時間(由于高運動電感)之間存在折衷,因為高運動電感是低運動電容的結果.(兩者的乘積或多或少是固定的.)這種相互依賴性部分地通過較小的運動電容與較小的并聯電容相關聯來減輕,這產生較大的負電阻并由此改善啟動時間.
啟動時間是電池供電應用中的一個重要考慮因素,其中設備經常打開和關閉.較短的振蕩器啟動時間可減少低功率無線電系統(例如使用MAX7032收發器和MAX1472或MAX7058發射器的系統)的能源浪費.
頻率穩定性與溫度 隨著溫度的變化,所有晶振的共振頻率都不同.頻率變化的方式取決于切割晶體的角度.AT切割石英晶振的相對頻移與溫度的關系可以表示為三次多項式.
Δf/f0=A0+A1(T-T0)+A2(T-T0)2+A3(T-T0)3
其中系數A0至A3是切割角度的函數.
頻率穩定性在使用晶體作為頻率參考的系統中很重要.對于高頻窄帶應用尤其如此.考慮863至870MHz歐洲ISM頻段中的25kHz信道.頻率漂移僅為5kHz(小于6ppm)可能導致通信故障或法規不合規.
即使在零容差晶體完全切割且不老化的情況下,在-40°C至85°C的耐高溫晶振中的"工業規格"溫度范圍內保持漂移遠低于6ppm也是不可能的.在這種情況下,帶有內部溫度傳感器和窄頻步分數N合成器的無線電系統,如MAX7049發射器,可用于補償已知的溫度變化.
正在載入評論數據...
相關資訊
- [2023-09-04]Abracon晶振5G小型蜂窩的時序參...
- [2023-08-31]CTS運輸產品手冊
- [2020-12-22]常用Oscillator輸出方式之間的性...
- [2019-07-25]負載電容決定晶振的共振頻率
- [2019-06-24]探討MEMS晶振第一和附加工藝的關...
- [2019-05-21]石英晶體諧振器縱向振動
- [2019-04-27]有源晶振啟動時間
- [2019-03-15]每個工程師應該知道有源晶振